FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 2: Linear Programming: Basic Concepts

Show Answer

Share

---

All types

Filters

Study FlashcardsPractice ExamLearn

Question 31

Multiple Choice

Review LaterAdd Note

Review Later

The production planner for a private label soft drink maker is planning the production of two soft drinks: root beer (R) and sassafras soda (S) . There are at most 12 hours per day of production time and 1,500 gallons per day of carbonated water available. A case of root beer requires 2 minutes of time and 5 gallons of water to produce, while a case of sassafras soda requires 3 minutes of time and 5 gallons of water. Profits for the root beer are $6.00 per case, and profits for the sassafras soda are $4.00 per case. The firm's goal is to maximize profits. What is the daily profit when producing the optimal amounts?

A) $960
B) $1,560
C) $1,800
D) $1,900
E) $2,520

Correct Answer

verified

Show Answer

Question 32

Multiple Choice

Review LaterAdd Note

Review Later

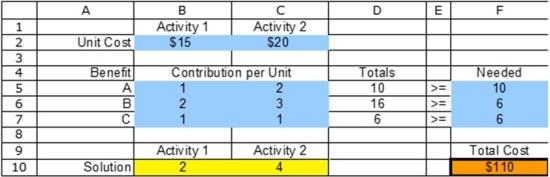Where is the objective cell located?

A) B2:C2
B) B2:C2, B5:C7, and F5:F7
C) B10:C10
D) F10
E) None of the answer choices are correct.

Correct Answer

verified

Show Answer

Question 33

True/False

Review LaterAdd Note

When solving a minimization problem graphically, it is generally the goal to move the objective function line out, away from the origin, as far as possible.

A local bagel shop produces bagels (B) and croissants (C) . Each bagel requires 6 ounces of flour, 1 gram of yeast, and 2 tablespoons of sugar. A croissant requires 3 ounces of flour, 1 gram of yeast, and 4 tablespoons of sugar. The company has 6,600 ounces of flour, 1,400 grams of yeast, and 4,800 tablespoons of sugar available for today's baking. Bagel profits are 20 cents each and croissant profits are 30 cents each. The shop wishes to maximize profits. What is the objective function?

Linear programming models can have either ≤ or ≥ inequality constraints but not both in the same problem.

When using the graphical method, the region that satisfies all of the constraints of a linear programming problem is called the:

The production planner for Fine Coffees, Inc. produces two coffee blends: American (A) and British (B) . He can only get 300 pounds of Colombian beans per week and 200 pounds of Dominican beans per week. Each pound of American blend coffee requires 12 ounces of Colombian beans and 4 ounces of Dominican beans, while a pound of British blend coffee uses 8 ounces of each type of bean. Profits for the American blend are $2.00 per pound, and profits for the British blend are $1.00 per pound. The goal of Fine Coffees, Inc. is to maximize profits. What is the constraint for Colombian beans?

The origin satisfies any constraint with a ≥ sign and a positive right-hand side.

The owner of Crackers, Inc. produces both Deluxe (D) and Classic (C) crackers. She only has 4,800 ounces of sugar, 9,600 ounces of flour, and 2,000 ounces of salt for her next production run. A box of Deluxe crackers requires 2 ounces of sugar, 6 ounces of flour, and 1 ounce of salt to produce. A box of Classic crackers requires 3 ounces of sugar, 8 ounces of flour, and 2 ounces of salt to produce. Profits are 40 cents for a box of Deluxe crackers and 50 cents for a box of Classic crackers. Cracker's, Inc. would like to maximize profits. What is the sugar constraint?

Using Excel's Solver add-in, find the optimal solution for the following problem? Maximize P = 3x + 8y Ssubject to $2 x + 4 y \leq 20$ $\begin{array} { c } 6 x + 3 y \leq 18 \\and~~x \geq 0 , y \geq 0 .\end{array}$

When formulating a linear programming problem on a spreadsheet, the Excel equation for each output cell can typically be expressed as a SUMPRODUCT function.

Which of the following could not be a constraint for a linear programming problem?

The operations manager for the Blue Moon Brewing Co. produces two beers: Lite (L) and Dark (D) . He can only get 675 gallons of malt extract per day for brewing and his brewing hours are limited to 8 hours per day. To produce a keg of Lite beer requires 2 minutes of time and 5 gallons of malt extract. Each keg of Dark beer needs 4 minutes of time and 3 gallons of malt extract. Profits for Lite beer are $3.00 per keg and profits for Dark beer are $2.00 per keg. The brewery's goal is to maximize profits. What is the daily profit when producing the optimal amounts?

Linear programming problems may have multiple goals or objectives specified.

A linear programming problem can have multiple optimal solutions.

The production planner for a private label soft drink maker is planning the production of two soft drinks: root beer (R) and sassafras soda (S) . There are at most 12 hours per day of production time and 1,500 gallons per day of carbonated water available. A case of root beer requires 2 minutes of time and 5 gallons of water to produce, while a case of sassafras soda requires 3 minutes of time and 5 gallons of water. Profits for the root beer are $6.00 per case, and profits for the sassafras soda are $4.00 per case. The firm's goal is to maximize profits. What is the objective function?

A feasible solution is one that satisfies all the constraints of a linear programming problem simultaneously.

A local bagel shop produces bagels (B) and croissants (C) . Each bagel requires 6 ounces of flour, 1 gram of yeast, and 2 tablespoons of sugar. A croissant requires 3 ounces of flour, 1 gram of yeast, and 4 tablespoons of sugar. The company has 6,600 ounces of flour, 1,400 grams of yeast, and 4,800 tablespoons of sugar available for today's baking. Bagel profits are 20 cents each and croissant profits are 30 cents each. The shop wishes to maximize profits. What is the daily profit when producing the optimal amounts?

An objective function represents a family of parallel lines.

Linear programming problems always involve either maximizing or minimizing an objective function.