A) 60%
B) 65%
C) 67%
D) 70%
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A researcher is planning to carry out a sample survey in order to estimate the proportion of people in a very large population of interest who have shopped online in the previous 6 months.A simple random sample is to be selected but there is debate about whether to select an SRS of size 500 or of size 1000.With respect to the sample proportion,which statement best describes what can be expected to happen using these two different sample sizes?
A) The statistic will be more biased in the sample of size 500,but the variability of the statistic will be smaller.
B) Using the larger sample size will reduce the bias of the statistic,but the spread of the sampling distribution will be greater.
C) The statistic from either sample size will be unbiased,but the sampling distribution of the statistic from the sample of size 1000 will show greater variability.
D) The statistic from either sample size will be unbiased,but the sampling distribution of the statistic from the sample of size 1000 will show less variability.
E) The sample size has no effect on the sampling distribution of the statistic because the population size is very large.
Correct Answer

verified
Correct Answer
verified
Short Answer
Should you have a cup of coffee to make you more alert when studying for a big test? A study on the effect of caffeine involved asking volunteers to take a memory test 20 minutes after drinking cola.Some volunteers were randomly assigned to drink caffeine-free cola,some were assigned regular cola (with caffeine),and others were assigned a mixture of the two (getting a half dose of caffeine).For each volunteer,a test score (the number of items recalled correctly)was recorded.The volunteers were not told which type of cola they had been given,but the researchers for the study prepared the cups of cola right on the spot (out of sight of the volunteers).The memory test had a total of 25 items on it.The average number of items recalled was 15 for the caffeine-free group,17 for the mixture group,and 16 for the regular cola group.Are the values 15,16,and 17 statistics or parameters?
Correct Answer

verified
Correct Answer
verified
Multiple Choice
In the construction industry,compressive strength of concrete is a crucial characteristic.Suppose for a particular residential construction job the concrete tested after 3 days should have a mean compression strength of = 3000 psi with a standard deviation of = 50 psi.It is known that compressive strength of concrete is Normally distributed.On a construction site,a sample of n = 5 specimens is selected and tested after 3 days.If the concrete has the desired characteristics,what is the probability that the sample mean 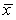 will be larger than 3060 psi?
will be larger than 3060 psi?
A) 0.996
B) 0.004
C) 0.885
D) 0.115
E) This can't be determined because the sample size n = 5 is much too small to rely on the Normal distribution for calculation of the required probability.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The scores of individual students on the American College Testing (ACT) ,college readiness assessment,have a Normal distribution with a mean of 18.6 and a standard deviation of 6.0.At Northside High,36 seniors take the test.Assume the scores at this school have the same distribution as national scores.What is the standard deviation of the sampling distribution of the sample mean score for a random sample of 36 students?
A) 1.0
B) 3.1
C) 6.0
D) 18.6
Correct Answer

verified
Correct Answer
verified
Multiple Choice
During the summer months,the prices of nonsmoking rooms with a king-sized bed in hotels in a certain area are roughly Normally distributed with a mean of $131.80 and a standard deviation of $29.12.What percentage of nonsmoking rooms with a king-sized bed cost more than $150?
A) 0.77%
B) 11.25%
C) 26.60%
D) 36.78%
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The figure below shows the Poisson distribution with a mean of 4.The Poisson distribution is an example of _________. 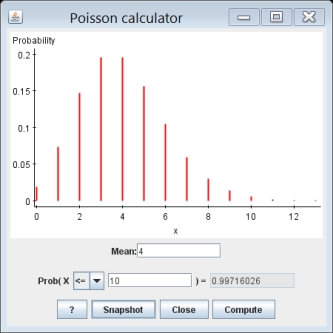
A) continuous probability distribution
B) discrete probability distribution
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let X represent the SAT total score of an entering freshman at University X.The random variable X is known to have a N(1200,90) distribution.Let Y represent the SAT total score of an entering freshman at University Y.The random variable Y is known to have a N(1215,110) distribution.A random sample of 100 freshmen is obtained from each university.Let 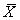 = the sample mean of the 100 scores from University X,and
= the sample mean of the 100 scores from University X,and 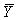 = the sample mean of the 100 scores from University Y.What is the probability that
= the sample mean of the 100 scores from University Y.What is the probability that 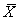 will be greater than
will be greater than 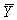 ?
?
A) 0.0475
B) 0.0869
C) 0.1456
D) 0.2266
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The length of time it takes to get through the security checks at a very large urban airport is a random variable with a mean of  20.6 minutes and a standard deviation of 11ec949d_bc0d_7f39_be2b_43474a185cb2_TB5065_00 8.4 minutes.A simple random sample of 36 airline passengers is to be observed going through security.For the passengers in the SRS,what is the approximate probability that the mean length of time for them to get through security will be less than 18 min?
20.6 minutes and a standard deviation of 11ec949d_bc0d_7f39_be2b_43474a185cb2_TB5065_00 8.4 minutes.A simple random sample of 36 airline passengers is to be observed going through security.For the passengers in the SRS,what is the approximate probability that the mean length of time for them to get through security will be less than 18 min?
A) 0.378
B) 0.186
C) 0.031
D) 0.314
E) Not within ± 0.005 of any of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A random variable X is Normally distributed with mean 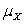 = 75 and
= 75 and 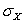 = 8.Let Y be a second Normally distributed random variable with mean
= 8.Let Y be a second Normally distributed random variable with mean 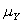 = 70 and
= 70 and 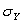 = 12.It is also known that X and Y are independent of one another.Let W be a random variable that is the difference between X and Y (i.e. ,W = X - Y) .What can be said about the distribution of W?
= 12.It is also known that X and Y are independent of one another.Let W be a random variable that is the difference between X and Y (i.e. ,W = X - Y) .What can be said about the distribution of W?
A) W is N(0,20)
B) W is N(5,20)
C) W is N(5,-4)
D) W is N(5,14.4)
E) W is N(0,14.4)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A population variable has a distribution with a mean of = 50 and a variance of 2 = 225.From this population a simple random sample of n observations is to be selected and the mean 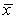 of the sample values calculated.If the population variable is known to be Normally distributed and the sample size used is to be n = 16,what is the probability that the sample mean will be between 48.35 and 55.74,that is,P(48.35
of the sample values calculated.If the population variable is known to be Normally distributed and the sample size used is to be n = 16,what is the probability that the sample mean will be between 48.35 and 55.74,that is,P(48.35 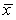 55.74) ?
55.74) ?
A) 0.393
B) 0.607
C) 0.937
D) 0.330
E) Not within ± 0.010 of any of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A study,conducted by Jackson et al.and published in the journal Cancer Causes and Control in 2009,examined 33,938 women aged 40 to 84 years old who resided in California and who reported having had a mammogram within the last 2 years.The researchers were interested in characteristics of women who routinely obtain mammograms,as suggested by the American Cancer Society,to detect breast cancer.The table below provides a column that refers to the sample size and provides characteristics of the 33,938 women who were included in the study who reported having had a mammogram. 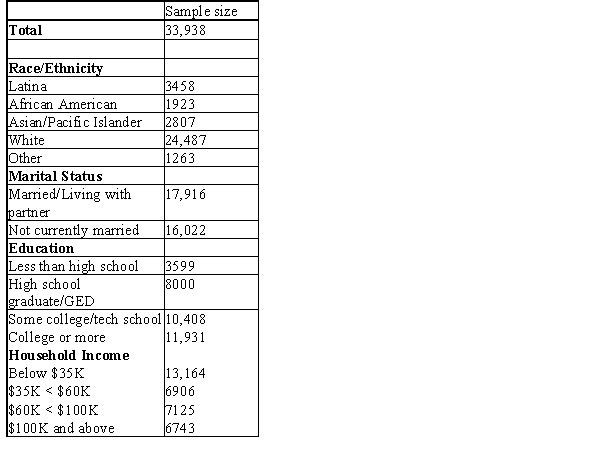 What proportion of the sample had a household income below $35K?
What proportion of the sample had a household income below $35K?
A) 13,164/33,938
B) 33,938/13,164
C) 13,164
D) 33,938
Correct Answer

verified
Correct Answer
verified
Multiple Choice
During the summer months,the prices of nonsmoking rooms with a king-sized bed in hotels in a certain area are roughly Normally distributed with a mean of $131.80 and a standard deviation of $29.12.A travel agent randomly selects prices of nonsmoking rooms with a king-sized bed from 15 hotels in the area.What is the probability that their average cost will be more than $150?
A) 0.0077
B) 0.1125
C) 0.2660
D) 0.3678
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let X represent the SAT total score of an entering freshman at University X.The random variable X is known to have a N(1200,90) distribution.Let Y represent the SAT total score of an entering freshman at University Y.The random variable Y is known to have a N(1215,110) distribution.A random sample of 100 freshmen is obtained from each university.Let 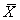 = the sample mean of the 100 scores from University X,and
= the sample mean of the 100 scores from University X,and 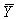 = the sample mean of the 100 scores from University Y.What is the distribution of the difference in sample means between University X and University Y:
= the sample mean of the 100 scores from University Y.What is the distribution of the difference in sample means between University X and University Y: 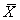 -
-  ?
?
A) N(-15,-20)
B) N(-15,14.2)
C) N(-15,142.1)
D) N(-15,200)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Let X represent the SAT total score of an entering freshman at University X.The random variable X is known to have a N(1200,90) distribution.Let Y represent the SAT total score of an entering freshman at University Y.The random variable Y is known to have a N(1215,110) distribution.A random sample of 100 freshmen is obtained from each university.Let 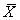 = the sample mean of the 100 scores from University X,and
= the sample mean of the 100 scores from University X,and  = the sample mean of the 100 scores from University Y.What is the probability that
= the sample mean of the 100 scores from University Y.What is the probability that 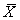 will be less than 1190?
will be less than 1190?
A) 0.0116
B) 0.1335
C) 0.4090
D) 0.4562
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The length of time it takes to get through the security checks at a very large urban airport is a random variable with a mean of = 20.6 minutes and a standard deviation of = 8.4 minutes.A simple random sample of 36 airline passengers is to be observed going through security.What is the variance 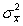 of the sampling distribution of the sample mean
of the sampling distribution of the sample mean 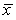 ?
?
A) 8.4 minutes
B) 20.6 minutes
C) 1.4 minute
D) None of the above
E) It is close to 8.4 minutes,but we can't be certain without having the data to determine it.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A gasoline tank for a certain car is designed to hold 15 gallons of gas.Suppose that the actual capacity of a randomly selected tank has a distribution that is approximately Normal with a mean of 15.0 gallons and a standard deviation of 0.15 gallons.The manufacturer of this gasoline tank considers the largest 2% of these tanks too large to put on the market.How large does a tank have to be to be considered too large?
A) 15 gallons
B) 15.31 gallons
C) 15.72 gallons
D) 16 gallons
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which of the following statements best describes a sampling distribution?
A) It is the distribution of the values of a particular variable that are observed in a random sample.
B) It is the distribution of the values of a variable in the population from which the sample is taken.
C) It is the distribution of the values of a statistic calculated from 1000 simple random samples displayed in a histogram.
D) It is the distribution of the values of a statistic that resembles the Normal distribution when the sample size is large.
E) It is the distribution of the values taken by a statistic in all possible samples of the same size from the same population.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Which histograms display a sampling distribution that is unbiased for estimating the proportion of women at a large university,which is known to be 45%?
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose you want to determine if there are differences in the average prices among items at three local supermarket chains.To reduce bias,how should you select the items to use in your study?
A) Choose items which you know are commonly purchased.
B) Randomly select an appropriate number of times from a list of all possible items in the supermarket.
C) Choose only brand-name items.
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 77
Related Exams