A) E(xt) is variable, Var(xt) is variable, and for any t, h ![]() 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
B) E(xt) is variable, Var(xt) is variable, and for any t, h ![]() 1, Cov(xt, xt+h) depends only on 't' and not on h.
1, Cov(xt, xt+h) depends only on 't' and not on h.
C) E(xt) is constant, Var(xt) is constant, and for any t, h![]() 1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
1, Cov(xt, xt+h) depends only on 'h' and not on 't'.
D) E(xt) is constant, Var(xt) is constant, and for any t, h![]() 1, Cov(xt, xt+h) depends only on 't' and not on 'h'.
1, Cov(xt, xt+h) depends only on 't' and not on 'h'.
Correct Answer

verified
Correct Answer
verified
True/False
Covariance stationarity focuses only on the first two moments of a stochastic process.
Correct Answer

verified
Correct Answer
verified
True/False
If a process is a covariance stationary process, then it will have a finite second moment.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose ut is the error term for time period 't' in a time series regression model the explanatory variables are xt = (xt1, xt2 …., xtk) . The assumption that the errors are contemporaneously homoskedastic implies that:
A) Var(ut|xt) = ![]() .
.
B) Var(ut|xt) = ![]() .
.
C) Var(ut|xt) =![]() 2.
2.
D) Var(ut|xt) =![]() .
.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Covariance stationary sequences where Corr(xt + xt+h) 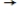 0 as
0 as 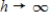 are said to be:
are said to be:
A) unit root processes.
B) trend-stationary processes.
C) serially uncorrelated.
D) asymptotically uncorrelated.
Correct Answer

verified
Correct Answer
verified
Showing 21 - 25 of 25
Related Exams