Filters
Question type
Study Flashcards

Use a graphing utility to graph the function below.Be sure to include at least two full periods. y=−2sin⁡(πx2−π4) y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right)


A) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right) A) B) C) D) E)
B) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right) A) B) C) D) E)
C) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right) A) B) C) D) E)
D) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right) A) B) C) D) E)
E) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = - \sqrt { 2 } \sin \left( \frac { \pi x } { 2 } - \frac { \pi } { 4 } \right) A) B) C) D) E)

Correct Answer

verifed

verified

For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v=0.85sin⁡(πt3) v = 0.85 \sin \left( \frac { \pi t } { 3 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0,and exhalation occurs when v < 0. ) ​ Find the time for one full respiratory cycle. ​


A) 7 sec
B) 9 sec
C) 3 sec
D) 8 sec
E) 6 sec

Correct Answer

verifed

verified

Find the period and amplitude. ​ Y = 7 sin 40x ​


A) Period: π;Amplitude: -7
B) Period: π;Amplitude: 17\frac { 1 } { 7 }
C) Period: π20\frac { \pi } { 20 } ;Amplitude: −17- \frac { 1 } { 7 }
D) Period: 2π;Amplitude: 1
E) Period: π20\frac { \pi } { 20 } ;Amplitude: 7

Correct Answer

verifed

verified

For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v=0.85sin⁡(πt4) v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​


A) For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​ A) B) C) D) E)
B) For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​ A) B) C) D) E)
C) For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​ A) B) C) D) E)
D) For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​ A) B) C) D) E)
E) For a person at rest,the velocity v (in liters per second) of airflow during a respiratory cycle (the time from the beginning of one breath to the beginning of the next) is given by​ v = 0.85 \sin \left( \frac { \pi t } { 4 } \right) , ​ Where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) Select the graph of this velocity function. ​ A) B) C) D) E)

Correct Answer

verifed

verified

Find a and d for the function f(x) = a sin x + d such that the graph of f(x) matches the graph below. Find a and d for the function f(x) = a sin x + d such that the graph of f(x) matches the graph below. 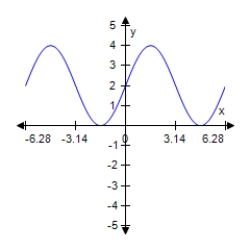A) a = 2;d = -1 B) a = 4;d = 1 C) a = -2;d = 1 D) a = 2;d = 2 E) a = 4;d = -3


A) a = 2;d = -1
B) a = 4;d = 1
C) a = -2;d = 1
D) a = 2;d = 2
E) a = 4;d = -3

Correct Answer

verifed

verified

Find the period and amplitude.​ y=45cos⁡4x5y = \frac { 4 } { 5 } \cos \frac { 4 x } { 5 } ​


A) Period: 2π;Amplitude: 1
B) Period: π2\frac { \pi } { 2 } ;Amplitude: 15\frac { 1 } { 5 }
C) Period: π;Amplitude: 54\frac { 5 } { 4 }
D) Period: π;Amplitude: 5
E) Period: 5π2\frac { 5 \pi } { 2 } ;Amplitude: 45\frac { 4 } { 5 }

Correct Answer

verifed

verified

After exercising for a few minutes,a person has a respiratory cycle for which the velocity of airflow is approximated by​ v=1.75sin⁡(πt3) v = 1.75 \sin \left( \frac { \pi t } { 3 } \right) , where t is the time (in seconds) . (Inhalation occurs when v > 0 and exhalation occurs when v < 0. ) ​ Find the time for one full respiratory cycle.​ ​


A) 6 sec
B) 2 sec
C) 7 sec
D) 3 sec
E) 8 sec

Correct Answer

verifed

verified

​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - π2\frac { \pi } { 2 } ) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​ ​


A) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​
B) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​
C) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​
D) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​
E) ​ ​Sketch the graph of the function below,being sure to include at least two full periods. ​ ​y = 2 cos​( x - \frac { \pi } { 2 } ) ​ ​ A) ​ B) ​ C) ​ D) ​ E) ​

Correct Answer

verifed

verified

Select the graph of the function.(Include two full periods. ) ​ y=cos⁡x4y = \cos \frac { x } { 4 } ​


A) Select the graph of the function.(Include two full periods. ) ​ y = \cos \frac { x } { 4 } ​ A) B) C) D) E)
B) Select the graph of the function.(Include two full periods. ) ​ y = \cos \frac { x } { 4 } ​ A) B) C) D) E)
C) Select the graph of the function.(Include two full periods. ) ​ y = \cos \frac { x } { 4 } ​ A) B) C) D) E)
D) Select the graph of the function.(Include two full periods. ) ​ y = \cos \frac { x } { 4 } ​ A) B) C) D) E)
E) Select the graph of the function.(Include two full periods. ) ​ y = \cos \frac { x } { 4 } ​ A) B) C) D) E)

Correct Answer

verifed

verified

When tuning a piano,a technician strikes a tuning fork for the A above middle C and sets up a wave motion that can be approximated by ​ Y = 0.001 sin 880πt, ​ Where t is the time (in seconds) . ​ What is the period of the function? ​


A) 1880\frac { 1 } { 880 } sec
B) 440 sec
C) 1440\frac { 1 } { 440 } sec
D) 880 sec
E) 88 sec

Correct Answer

verifed

verified

When tuning a piano,a technician strikes a tuning fork for the A above middle C and sets up a wave motion that can be approximated by ​ Y = 0.001 sin 850πt, ​ Where t is the time (in seconds) . ​ The frequency is given by f = 1 / p.What is the frequency of the note? ​


A) 85 cycles/sec
B) 1425\frac { 1 } { 425 } cycles/sec
C) 1850\frac { 1 } { 850 } cycles/sec
D) 850 cycles/sec
E) 425 cycles/sec

Correct Answer

verifed

verified

Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​


A) Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​ A) B) C) D) E)
B) Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​ A) B) C) D) E)
C) Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​ A) B) C) D) E)
D) Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​ A) B) C) D) E)
E) Use a graphing utility to select the graph of the function.Include two full periods. ​ Y = -2 sin (2x + π) ​ A) B) C) D) E)

Correct Answer

verifed

verified

Select the graph of the function.(Include two full periods. ) ​ y=−6cos⁡πx3y = - 6 \cos \frac { \pi x } { 3 } ​


A) Select the graph of the function.(Include two full periods. ) ​ y = - 6 \cos \frac { \pi x } { 3 } ​ A) B) C) D) E)
B) Select the graph of the function.(Include two full periods. ) ​ y = - 6 \cos \frac { \pi x } { 3 } ​ A) B) C) D) E)
C) Select the graph of the function.(Include two full periods. ) ​ y = - 6 \cos \frac { \pi x } { 3 } ​ A) B) C) D) E)
D) Select the graph of the function.(Include two full periods. ) ​ y = - 6 \cos \frac { \pi x } { 3 } ​ A) B) C) D) E)
E) Select the graph of the function.(Include two full periods. ) ​ y = - 6 \cos \frac { \pi x } { 3 } ​ A) B) C) D) E)

Correct Answer

verifed

verified

Write an equation for the function that is described by the given characteristics. ​ A cosine curve with a period of π,an amplitude of 6,a left phase shift of π,and a vertical translation down 43\frac { 4 } { 3 } units. ​


A) y=6cos⁡(2x+π) −43y = 6 \cos ( 2 x + \pi ) - \frac { 4 } { 3 }
B) y=6cos⁡(2x+2π) −43y = 6 \cos ( 2 x + 2 \pi ) - \frac { 4 } { 3 }
C) y=6cos⁡(2x+2π) +43y = 6 \cos ( 2 x + 2 \pi ) + \frac { 4 } { 3 }
D) y=6cos⁡(x+2π) −43y = 6 \cos ( x + 2 \pi ) - \frac { 4 } { 3 }
E) y=6cos⁡(x+π) −43y = 6 \cos ( x + \pi ) - \frac { 4 } { 3 }

Correct Answer

verifed

verified

Find a,b,and c for the function f(x) = a cos (bx - c) such that the graph of f(x) matches the graph below. Find a,b,and c for the function f(x) = a cos (bx - c) such that the graph of f(x) matches the graph below. 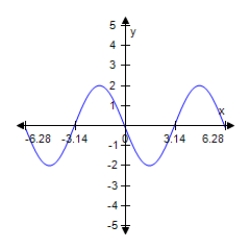A) a = -2;b = -1;c= - \frac { 3 } { 2 } B) a = 4;b = 1;c = π C) a = 1;b = 2;c = -1 D) a = 2;b = 1;c = -π E) a = 2;b = 1;c = - \frac { 1 } { 2 } π


A) a = -2;b = -1;c= −32- \frac { 3 } { 2 }
B) a = 4;b = 1;c = π
C) a = 1;b = 2;c = -1
D) a = 2;b = 1;c = -π
E) a = 2;b = 1;c = −12- \frac { 1 } { 2 } π

Correct Answer

verifed

verified

Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1


A) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1 A) B) ​ C) ​ D) ​ E) ​
B) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1 A) B) ​ C) ​ D) ​ E) ​ ​
C) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1 A) B) ​ C) ​ D) ​ E) ​ ​
D) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1 A) B) ​ C) ​ D) ​ E) ​ ​
E) Use a graphing utility to graph the function below.Be sure to include at least two full periods. y = 4 sin (x - 5π) + 1 A) B) ​ C) ​ D) ​ E) ​ ​

Correct Answer

verifed

verified

The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C=30.5+21.6sin⁡(2πt365+10.3) C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​


A) The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​ A) B) C) D) E)
B) The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​ A) B) C) D) E)
C) The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​ A) B) C) D) E)
D) The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​ A) B) C) D) E)
E) The daily consumption C (in gallons) of diesel fuel on a farm is modeled by​ C = 30.5 + 21.6 \sin \left( \frac { 2 \pi t } { 365 } + 10.3 \right) , ​ Where t is the time (in days) ,with t = 1 corresponding to January 1. Use a graphing utility to select the graph of the model. ​ A) B) C) D) E)

Correct Answer

verifed

verified

Showing 21 - 37 of 37

Related Exams

Exam 1

Rectangular Coordinates

69 Questions

Exam 2

Graphs of Equations

63 Questions

Exam 3

Linear Equations in Two Variables

61 Questions

Exam 4

Functions

53 Questions

Exam 5

Analyzing Graphs of Functions

56 Questions

Exam 6

A Library of Parent Functions

50 Questions

Exam 7

Transformations of Functions

32 Questions

Exam 8

Combinations of Functions Composite Functions

58 Questions

Exam 9

Inverse Functions

59 Questions

Exam 10

Mathematical Modeling and Variation

49 Questions

Exam 11

Quadratic Functions and Models

61 Questions

Exam 12

Polynomial Functions of Higher Degree

63 Questions

Exam 13

Polynomial and Synthetic Division

76 Questions

Exam 14

Complex Numbers

59 Questions

Exam 15

Zeros of Polynomial Functions

49 Questions

Exam 16

Rational Functions

96 Questions

Exam 17

Nonlinear Inequalities

56 Questions

Exam 18

Exponential Functions and Their Graphs

59 Questions

Exam 19

Logarithmic Functions and Their Graphs

64 Questions

Exam 20

Properties of Logarithms

57 Questions

Exam 21

Exponential and Logarithmic Equations

51 Questions

Exam 22

Exponential and Logarithmic Models

56 Questions

Exam 23

Radian and Degree Measure

52 Questions

Exam 24

Trigonometric Functions The Unit Circle

50 Questions

Exam 25

Right Triangle Trigonometry

56 Questions

Exam 26

Trigonometric Functions of Any Angle

53 Questions

Exam 28

Graphs of Other Trigonometric Functions

51 Questions

Exam 29

Inverse Trigonometric Functions

50 Questions

Exam 30

Applications and Models

52 Questions

Exam 31

Using Fundamental Identities

60 Questions

Exam 32

Verifying Trigonometric Equations

46 Questions

Exam 33

Solving Trigonometric Equations

54 Questions

Exam 34

Sum and Difference Formulas

62 Questions

Exam 35

Multiple Angle and Product to Sum Formulas

50 Questions

Exam 36

Law of Sines

43 Questions

Exam 37

Law of Cosines

43 Questions

Exam 38

Vectors in the Plane

50 Questions

Exam 39

Vectors and Dot Products

67 Questions

Exam 40

Trigonometric Form of a Complex Number

104 Questions

Exam 41

Linear and Nonlinear Systems of Equations

58 Questions

Exam 42

Two Variable Linear Systems

49 Questions

Exam 43

Multivariable Linear Systems

54 Questions

Exam 44

Partial Fractions

48 Questions

Exam 45

Systems of Inequalities

50 Questions

Exam 46

Linear Programming

50 Questions

Exam 47

Matrices and Systems of Equations

65 Questions

Exam 48

Operations With Matrices

59 Questions

Exam 49

The Inverse of a Square Matrix

59 Questions

Exam 50

The Determinant of a Square Matrix

52 Questions

Exam 51

Applications of Matrices and Determinants

54 Questions

Exam 52

Sequences and Series

68 Questions

Exam 53

Arithmetic Sequences and Partial Sums

52 Questions

Exam 54

Geometric Sequences and Series

67 Questions

Exam 55

Mathematical Induction

48 Questions

Exam 56

The Binomial Theorem

67 Questions

Exam 57

Counting Principles

55 Questions

Exam 58

Probability

47 Questions

Exam 59

Lines

50 Questions

Exam 60

Introduction to Conics Parabolas

124 Questions

Exam 61

Ellipses

68 Questions

Exam 62

Hyperbolas

62 Questions

Exam 63

Rotation of Conics

52 Questions

Exam 64

Parametric Equations

50 Questions

Exam 65

Polar Coordinates

50 Questions

Exam 66

Polar Equations of Conics

50 Questions

Exam 67

Graphs of Polar Equations

49 Questions

Show Answer