FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 23: Use and Abuse of Statistical Inference

Show Answer

Share

---

All types

Filters

Study FlashcardsPractice ExamLearn

Question 1

Multiple Choice

Review LaterAdd Note

Review Later

Which is more informative: confidence intervals or significance tests?

A) Significance tests, because they use a P-value.
B) Significance tests, because they compare two hypotheses.
C) Confidence intervals, because they estimate the population parameter.
D) Confidence intervals, because they use sample information.
E) Significance tests, because they use a P-value, and they compare two hypotheses.

Correct Answer

verified

C

Question 2

Multiple Choice

Review LaterAdd Note

Review Later

Which of the following would be most helpful in assessing the practical significance of a test of hypotheses about a proportion?

A) Test the hypotheses using significance level  = 0.001.
B) Report the P-value of your test.
C) Take another sample and retest just to make sure the results are not due to chance.
D) Construct a 99% confidence interval for the proportion in order to see the magnitude of the proportion.

Correct Answer

verified

Show Answer

Question 3

Multiple Choice

Review LaterAdd Note

A researcher wishes to determine if students are able to complete a certain puzzle more quickly while exposed to a pleasant floral scent. Suppose the time (in seconds) needed for high school students to complete the puzzle while exposed to the scent follows a normal distribution with mean  and standard deviation  = 4. Suppose also, that in the general population of all high school students, the time needed to complete the puzzle follows a normal distribution with mean 80 and standard deviation  = 4. The researcher, therefore, decides to test the hypotheses: H₀:  = 80 H_a:  < 80 To do so, the researcher has 10,000 high school students complete the puzzle in the presence of the floral scent. The mean time for these students is 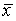= 79.8 seconds and the P-value is less than 0.0001. It is appropriate to conclude which of the following?

A popular brand of AAA batteries has an effective use time of 12.3 hours, on average. A startup company claims that their AAA batteries last longer. The startup company tested 24,000 of their new batteries and computed a mean effective use time of 12.32 hours. Although the difference is quite small (72 seconds-or just over a minute) , the effect was statistically significant (P-value < 0.0001) . The most likely explanation for a 72-second difference being reported as statistically significant is

In assessing the validity of any test of hypotheses, it is good practice to

Coleman surveys a random sample of city residents and uses a 95% confidence interval to estimate the proportion of all city residents who plan to vote in an upcoming election. Emma isn't satisfied with 95% confidence. She wants to use a 99% confidence interval, but she doesn't want it to be any wider that Coleman's 95% confidence interval. In order to achieve this, Emma must

A government agency funds research on cancer. The agency funds 25 research projects, all of which are testing various drugs to see if they are effective in reducing brain tumors. One of the projects (project number 12) finds that the drug they are studying significantly reduces the size of tumors with a P-value of 0.028. The other 24 projects found no significant effects (P-values all greater than 0.05) of the drugs that they studied. Is it proper to conclude that the drug in project number 12 is effective in reducing the size of brain tumors?

An engineer designs an improved light bulb. The previous design had an average lifetime of 1200 hours. The new bulb had a lifetime of 1200.2 hours, using a sample of 40,000 bulbs. Although the difference is quite small, the effect was statistically significant. The most likely explanation is

A popular brand of AAA batteries has an effective use time of 12.3 hours, on average. A startup company claims that their AAA batteries last longer. The startup company tested 24,000 of their new batteries and computed a mean effective use time of 12.32 hours. Although the difference is quite small (72 seconds-or just over a minute) , the effect was statistically significant (P-value < 0.0001) . It is appropriate to conclude which of the following?

An anthropologist wants to compare the average lifespans of the current residents of a village in Uganda to that of those who resided there 100 years ago. Five residents who died this year are randomly selected to be compared to five residents who died 100 years ago. Although the difference in average lifespans is 16.4 years, the results are not statistically significant (P-value = 0.2169) . The most likely explanation is

Due to a budget consideration, a researcher is asked to decrease the number of subjects in an experiment. Which of the following will occur?

A medical researcher is working on a new treatment for a certain type of cancer. The average survival time after diagnosis on the standard treatment is two years. In an early trial, she tries the new treatment on three subjects who have an average survival time after diagnosis of four years. Although the survival time has doubled, the results are not statistically significant even at the 0.10 significance level. The most likely explanation is

The New You Cancer Center (not a real entity) promotes therapies outside ordinary, Western medicine: meditation, crystals, yoga-and 197 others. To investigate the efficacy of these therapies, a researcher hired by the center conducted a study with 150 adult subjects who were patients at the center. At the end of the study, the effect of the 200 therapies on the subjects were measured. Nine of these therapies were found to have made the subjects' "quality of life metric" significantly better (in the sense of statistical significance) at the  = 0.05 level compared to a control group, and one therapy was significantly better at the  = 0.01 level compared to a control group. It would be correct to conclude:

A television show runs a call-in survey each morning. One January morning the show asked its viewers whether they were optimistic or pessimistic about the economy in the coming year. The majority of those phoning in their responses answered "pessimistic" and the show reported the results as statistically significant. We may safely conclude

A researcher wishes to determine if students are able to complete a certain puzzle more quickly while exposed to a pleasant floral scent. Suppose the time (in seconds) needed for high school students to complete the puzzle while exposed to the scent follows a normal distribution with mean  and standard deviation  = 4. Suppose also, that in the general population of all high school students, the time needed to complete the puzzle follows a normal distribution with mean 80 and standard deviation  = 4. The researcher, therefore, decides to test the hypotheses: H₀:  = 80 H_a:  < 80 To do so, the researcher has 10,000 high school students complete the puzzle in the presence of the floral scent. The mean time for these students is 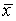= 79.8 seconds and the P-value is less than 0.0001. Suppose that two high school students decide to see if they get the same results as the researcher. They both do the puzzle while in the presence of the pleasant floral scent. The mean of their times is 80.2 seconds, the same as that of the researcher. It is appropriate to conclude which of the following:

In testing hypotheses, if the consequences of rejecting the null hypothesis are very serious, we should

How small must a P-value be in order to consider it convincing evidence against the null hypothesis?

Suppose one lives in a fairly wealthy Western nation where life expectancy follows a normal distribution with mean  = 80 and standard deviation  = 15. One reads a report that claims that 10,000 subjects who took part in a national program for improving one's lifespan lived significantly longer (at the 0.05 level of significance) than the population as a whole. In order to determine if the improvement is of practical significance, one should: