FiltersDone

Question type

Essay

Multiple Choice

Short Answer

True False

Matching

Exam 4: Linear Programming Sensitivity Analysis

Show Answer

Share

---

All types

Filters

Study Flashcards

Question 31

Multiple Choice

Review LaterAdd Note

Review Later

Surplus is typically associated with which type of constraints?

A) ≤
B) ≥
C) =
D) ≠
E) ±

Correct Answer

verified

Show Answer

Question 32

True/False

Review LaterAdd Note

Review Later

The Sensitivity Report typically analyses the impact of simultaneous changes in the objective function coefficients and right-hand side constraint values on the optimal solution.

Correct Answer

verified

Show Answer

Question 33

Multiple Choice

Review LaterAdd Note

Use this information,along with its associated Sensitivity Report,to answer the following questions. A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table. $\begin{array} { | c | c | c | c | } \hline \underline { \text { Product } } & \frac { \text { Material 1 } } { ( \mathrm { lbs } ) } & \frac { \text { Material 2 } } { ( \mathrm { lbs } . ) } & \text { Labor (hours) } \\\hline \underline { \underline { \mathrm { A } } } & \underline { 3 } & \underline { 2 } & \underline { 4 } \\\hline \underline { \mathrm { B } } & \underline { 1 } & \underline { 4 } & \underline { 2 } \\\hline \underline { \mathrm { C } } & \underline { 5 } & \underline { \text { none } } & \underline { 3.5 } \\\hline\end{array}$ Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week. 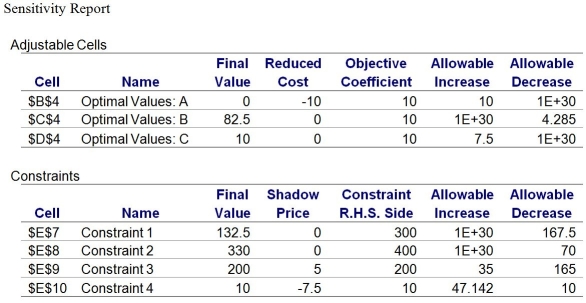$\begin{array}{l}\text { Formulation }\\\begin{array} { l l } \ { \text { Max } } & 10 \mathrm {~A} + 10 \mathrm {~B} + 10 \mathrm { C } \\\text { Subject to: } & \\& 3 \mathrm {~A} + \mathrm { B } + 5 \mathrm { C } \leq 300 \text { (constraint \#1) } \\& 2 \mathrm {~A} + 4 \mathrm {~B} \leq 400 \text { (constraint \#2) } \\& 4 \mathrm {~A} + 2 \mathrm {~B} + 3.5 \mathrm { C } \leq 200 \text { (constraint \#3) } \\& \mathrm { C } \geq 10 \text { (constraint \#4) } \\& \mathrm { A } , \mathrm { B } , \mathrm { C } \geq 0\end{array}\end{array}$ -Suppose that we force the production of one unit of product A.The new objective function value will be

Assume that the reduced cost of a decision variable is -$20 for a maximization problem.This implies that: