A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people.In an isolated town of 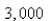 inhabitants,
inhabitants, 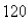 people have a disease at the beginning of the week and
people have a disease at the beginning of the week and 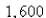 have it at the end of the week.How long does it take for
have it at the end of the week.How long does it take for 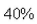 of the population to be infected? Select the correct Answer
of the population to be infected? Select the correct Answer
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Essay
A common inhabitant of human intestines is the bacterium 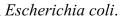 A cell of this bacterium in a nutrient-broth medium divides into two cells every
A cell of this bacterium in a nutrient-broth medium divides into two cells every  The initial population of a culture is
The initial population of a culture is  cells.Find the number of cells after
cells.Find the number of cells after 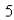 hours.
hours.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the differential equation. 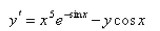
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Essay
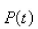 be the performance level of someone learning a skill as a function of the training time
be the performance level of someone learning a skill as a function of the training time 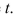 The graph of P is called a
The graph of P is called a 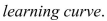 We propose the differential equation
We propose the differential equation  as a reasonable model for learning, where r is a positive constant.Solve it as a linear differential equation.
as a reasonable model for learning, where r is a positive constant.Solve it as a linear differential equation.
Correct Answer

verified
Correct Answer
verified
Essay
In the circuit shown in Figure, a generator supplies a voltage of  volts, the inductance is
volts, the inductance is 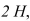 the resistance is 40
the resistance is 40 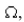 , and
, and 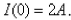 Find the current 0.2 s after the switch is closed.Round yourAnswer to two decimal places.
Find the current 0.2 s after the switch is closed.Round yourAnswer to two decimal places. 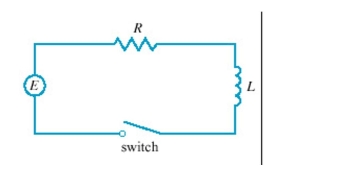
Correct Answer

verified
Correct Answer
verified
Essay
A sum of 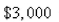 s invested at
s invested at 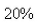 interest.If
interest.If 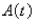 is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by
is the amount of the investment at time t for the case of continuous compounding, write a differential equation and an initial condition satisfied by 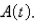
Correct Answer

verified
Correct Answer
verified
Multiple Choice
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people.In an isolated town of 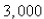 inhabitants,
inhabitants, 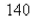 people have a disease at the beginning of the week and
people have a disease at the beginning of the week and 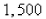 have it at the end of the week.How long does it take for
have it at the end of the week.How long does it take for 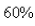 of the population to be infected? Select the correct Answer
of the population to be infected? Select the correct Answer
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select the correct Answer: for each question.
-Solve the differential equation. 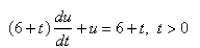
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Suppose that a population grows according to a logistic model with carrying capacity 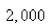 and
and 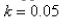 per year.Choose the logistic differential equation for these data.
per year.Choose the logistic differential equation for these data.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
A phase trajectory is shown for populations of rabbits  and foxes
and foxes  Describe how each population changes as time goes by.Select the correct Answer
Describe how each population changes as time goes by.Select the correct Answer 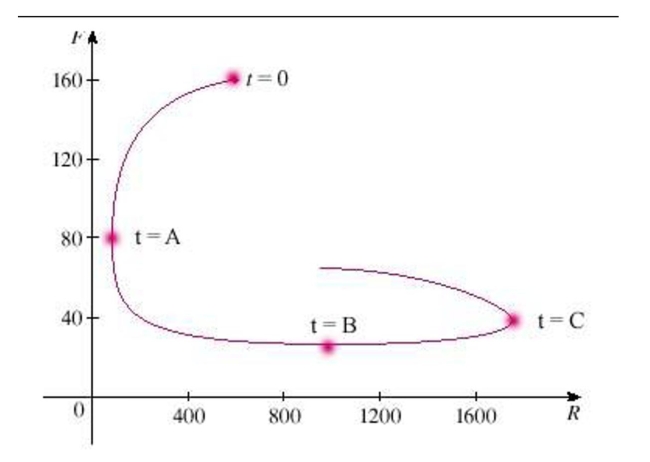 Select the correct statement.
Select the correct statement.
A) At ![]() the number of rabbits rebounds to 500.
the number of rabbits rebounds to 500.
B) At ![]() the number of foxes reaches a maximum of about 2400.
the number of foxes reaches a maximum of about 2400.
C) At ![]() the population of foxes reaches a minimum of about 30.
the population of foxes reaches a minimum of about 30.
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the differential equation.Select the correct Answer 
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the initial-value problem. 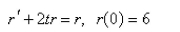
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Essay
A curve passes through the point 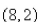 and has the property that the slope of the curve at every point P is
and has the property that the slope of the curve at every point P is 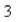 times the y-coordinate P.What is the equation of the curve?
times the y-coordinate P.What is the equation of the curve?
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the differential equation. 
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Essay
Biologists stocked a lake with  fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be
fish and estimated the carrying capacity (the maximal population for the fish of that species in that lake) to be 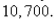 The number of fish tripled in the first year.Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
The number of fish tripled in the first year.Assuming that the size of the fish population satisfies the logistic equation, find an expression for the size of the population after t years.
Correct Answer

verified
Correct Answer
verified
Essay
One model for the spread of an epidemic is that the rate of spread is jointly proportional to the number of infected people and the number of uninfected people.In an isolated town of 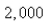 inhabitants,
inhabitants, 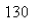 people have a disease at the beginning of the week and
people have a disease at the beginning of the week and  have it at the end of the week.How long does it take for
have it at the end of the week.How long does it take for 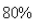 of the population to be infected?
of the population to be infected?
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine whether the differential equation is linear. 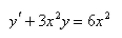
A) the equation is not linear
B) the equation is linear
Correct Answer

verified
Correct Answer
verified
Essay
Find the orthogonal trajectories of the family of curves. 
Correct Answer

verified
Correct Answer
verified
Essay
Choose the differential equation corresponding to this direction field. 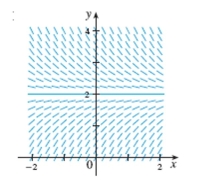
Correct Answer

verified
Correct Answer
verified
Showing 61 - 80 of 160
Related Exams