A)
B)
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the phase shift of the function. -
A) units up
B) units to the right
C) units to the left
D) units down
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -Ignoring friction, the time, (in seconds) , required for a block to slide down an inclined plane is given by the formula where is the length of the base in feet and feet per second is the acceleration of gravity. How long does it take a block to slide down an inclined plane with a base of 12 feet at an angle of ? Round your answer to three decimal places.
A)
B)
C)
D)
F) B) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π. -
A)
B)
C)
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .

A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
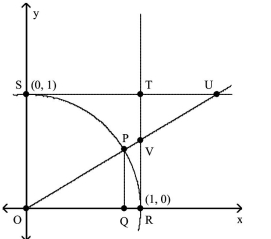
Solve the problem.
-Let angle be designated . Angles and are right angles. If , find the exact length of US.
A)
B) 0
C) 1
D)
F) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
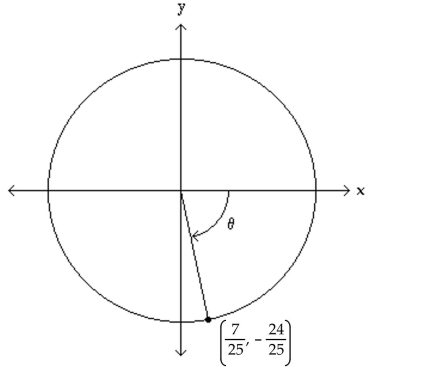
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find .
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the exact circular function value. -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The minute hand of a clock is 14 inches long. What distance does its tip move in 23 minutes? Give an exact answer.
A) .
B) .
C) .
D) .
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the value of s in the interval [0, π/2] that makes the statement true. Round to four decimal places. -
A)
B)
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Convert the degree measure to radians, correct to four decimal places. Use 3.1416 for π. -
A)
B)
C)
D)
F) A) and D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The voltage in an electrical circuit is given by , where is time measured in seconds. Find the amplitude.
A)
B) 140
C)
D)
F) B) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a table or a calculator to evaluate the function. Round to four decimal places. -
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
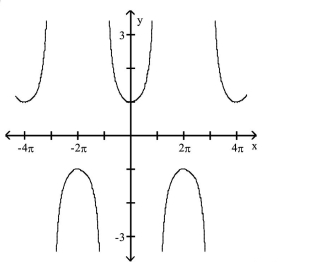
Determine the equation of the graph.
-
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
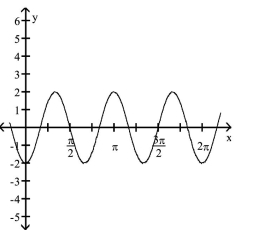
The function graphed is of the form y = a sin bx or y = a cos bx, where b > 0. Determine the equation of the graph.
-
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A spring with a spring constant of 6 and a 1-unit mass attached to it is stretched and released. What is the equation for the resulting oscillatory motion?
A)
B)
C)
D)
F) All of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The figure shows an angle θ in standard position with its terminal side intersecting the unit circle. Evaluate the
indicated circular function value of θ.
-Find
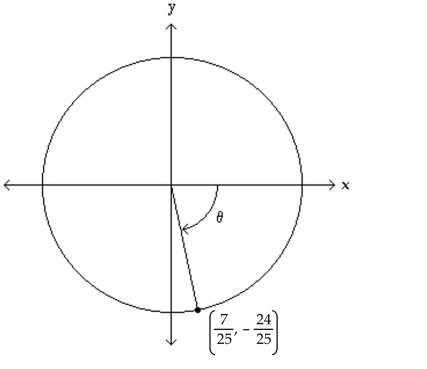
A)
B)
C)
D)
F) A) and C)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -The minimum length of a highway sag curve can be computed by where is the downhill grade in degrees is the uphill grade in degrees is the safe stopping distance for a given speed limit, is the height of the headlights, and is the alignment of the headlights in degrees. Compute for a 55 -mph speed limit, where , , and . Round your answer to the nearest foot.
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A sensor light installed on the edge of a home can detect motion for a distance of . in front and with a range of motion of . Over what area will the sensor detect motion and become illuminated? Round to the nearest hundredth.
A)
B)
C)
D)
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -An object is spinning around a circle with a radius of 19 centimeters. If in 9 seconds a central angle of radian has been covered, what is the linear speed of the object?
A) per sec
B) per sec
C) per sec
D) per sec
F) A) and B)
Correct Answer

verified
Correct Answer
verified
Showing 241 - 260 of 289
Related Exams