A) 1.82 mi
B) 4.48 mi
C) 7.37 mi
D) 3 mi
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the triangle. If necessary, round the answer to two decimal places.
-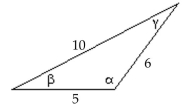
A) 3.52
B) 11.4
C) 235.46
D) 51.38
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -From the edge of a 1000-foot cliff, the angles of depression to two cars in the valley below are 21° and 28°. How far apart are the cars? Round your answers to the nearest 0.1 ft.
A) 724.5 ft
B) 713.4 ft
C) 724.4 ft
D) 714.4 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A guy wire to the top of a tower makes an angle of 64° with the level ground. At a point 26 feet farther from the base of the tower and in line with the base of the wire, the angle of elevation to the top of the tower is 27°. What Is the length of the guy wire?
A) 38.83 ft
B) 13.13 ft
C) 51.47 ft
D) 19.61 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the triangle. If necessary, round the answer to two decimal places. -
A) 3.52
B) 3.50
C) 3.51
D) 3.53
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the triangle. If necessary, round the answer to two decimal places. -A new homeowner has a triangular-shaped back yard. Two of the three sides measure 65 ft and 80 ft and form an included angle of 125°. The owner wants to approximate the area of the yard, so that he can determine the Amount of fertilizer and grass seed to be purchased. Find the area of the yard rounded to the nearest square Foot.
A) 5200 sq. ft
B) 2130 sq. ft
C) 4260 sq. ft
D) 2129 sq. ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the triangle. If necessary, round the answer to two decimal places.
-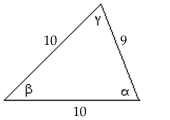
A) 84.97
B) 10.55
C) 457.58
D) 40.19
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A surveyor is measuring the distance across a small lake. He has set up his transit on one side of the lake 90 feet from a piling that is directly across from a pier on the other side of the lake. From his transit, the angle between The piling and the pier is 55°. What is the distance between the piling and the pier to the nearest foot?
A) 74 ft
B) 63 ft
C) 129 ft
D) 52 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Two sides of a right triangle ABC (C is the right angle) are given. Find the indicated trigonometric function of the given angle. Give exact answers with rational denominators. -Find when and .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -Find the area of the Bermuda Triangle if the sides of the triangle have the approximate lengths 844 miles, 921 miles, and 1,314 miles.
A) 510,414 mi
B) 386,440 mi
C) 1,545,758 mi
D) 489,843 mi
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -In flying the 81 miles from Champaign to Peoria, a student pilot sets a heading that is 9° off course and maintains an average speed of 96 miles per hour. After 15 minutes, the instructor notices the course error and Tells the student to correct his heading. Through what angle will the plane move to correct the heading and how Many miles away is Peoria when the plane turns?
A) 12.7°; 72.23 mi
B) 12.7°; 57.42 mi
C) 167.3°; 72.23 mi
D) 167.3°; 57.42 mi
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -Given a triangle with a = 9, b = 11, , what is (are) the possible length(s) of c? Round your answer to two decimal places.
A) 16.42 or 2.44
B) 16.42 or 3.41
C) 6.61
D) 14.21
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The displacement d (in meters) of an object at time t (in seconds) is given. Describe the motion of the object. What is the maximum displacement from its resting position, the time required for one oscillation, and the frequency? -
A) simple harmonic; oscillations/sec
B) simple harmonic; oscillations/sec
C) simple harmonic; sec; oscillations/sec
D) simple harmonic; oscillations/sec
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -Two points A and B are on opposite sides of a building. A surveyor selects a third point C to place a transit. Point C is 52 feet from point A and 68 feet from point B. The angle ACB is 53°. How far apart are points A and B?
A) 97.2 ft
B) 107.6 ft
C) 72.1 ft
D) 55.4 ft
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the problem. -A tree casts a shadow of 26 meters when the angle of elevation of the sun is 24°. Find the height of the tree to the nearest meter.
A) 10 m
B) 11 m
C) 12 m
D) 13 m
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the area of the triangle. If necessary, round the answer to two decimal places. -a = 6, b = 6, c = 7
A) 15.54
B) 17.06
C) 18.25
D) 21.14
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Two sides and an angle are given. Determine whether the given information results in one triangle, two triangles, or no triangle at all. Solve any triangle(s) that results. -
A) one triangle
B) one triangle
C) one triangle
D) no triangle
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle using the information given. Round answers to two decimal places, if necessary.  - Find , and .
- Find , and .
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
the motion is simple harmonic with period T, write an equation that relates the displacement d of the object from its rest
position after t seconds. Also assume that the positive direction of the motion is up.An object attached to a coiled spring is pulled down a distance a from its rest position and then released. Assuming that
-a = 17; T = 5 seconds A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Showing 61 - 80 of 103
Related Exams