A) 2
B)
C) 1
D) 3
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the length of the arc on a circle of radius r intercepted by a central angle θ. Round answer to two decimal places. -The minute hand of a clock is 4 inches long. How far does the tip of the minute hand move in 35 minutes? If necessary, round the answer to two decimal places.
A) inches
B) inches
C) inches
D) inches
Correct Answer

verified
Correct Answer
verified
Multiple Choice
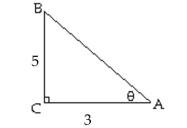
Use the Pythagorean Theorem to find the length of the missing side.Then find the indicated trigonometric function
of the given angle. Give an exact answer with a rational denominator.
-Find
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use a calculator to find the value of the expression rounded to two decimal places. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Understand the Graphs of y = csc x and y = sec x
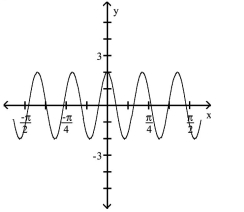
Use the graph to obtain the graph of the reciprocal function. Give the equation of the function for the graph that
you obtain.
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the amplitude or period as requested. Graph Variations of y = cos x -Amplitude of
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use reference angles to find the exact value of the expression. Do not use a calculator. -
A)
B)
C) -2
D) )
Correct Answer

verified
Correct Answer
verified
Multiple Choice
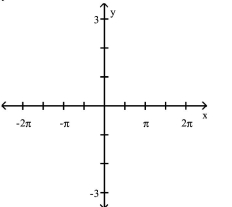
Graph Variations of y = csc x and y = sec x
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Determine the amplitude or period as requested. -Period of
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
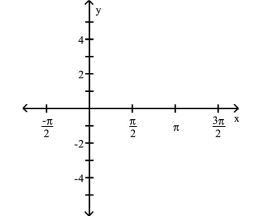
Additional Concepts
-
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use reference angles to find the exact value of the expression. Do not use a calculator. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle shown in the figure. Round lengths to one decimal place and express angles to the nearest
tenth of a degree. 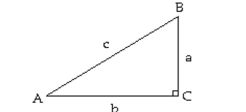 -
-
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle shown in the figure. Round lengths to one decimal place and express angles to the nearest
tenth of a degree.  -A building 150 feet tall casts a 100 foot long shadow. If a person stands at the end of the shadow and looks up to the top of the building, what is the angle of the person's eyes to the top of the building (to the nearest hundredth of a degree) ? (Assume the person's eyes are 5 feet above ground level.)
-A building 150 feet tall casts a 100 foot long shadow. If a person stands at the end of the shadow and looks up to the top of the building, what is the angle of the person's eyes to the top of the building (to the nearest hundredth of a degree) ? (Assume the person's eyes are 5 feet above ground level.)
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the function.
-
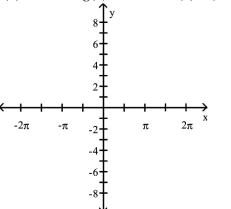
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
θ is an acute angle and sin θ and cos θ are given. Use identities to find the indicated value. -
A) 1
B) 0
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph Variations of y = cot x
-
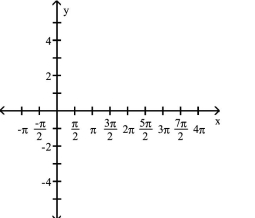
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Pythagorean Theorem to find the length of the missing side.Then find the indicated trigonometric function
of the given angle. Give an exact answer with a rational denominator.
-Find .
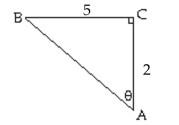
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the length of the arc on a circle of radius r intercepted by a central angle θ. Round answer to two decimal places. - inches,
A) inches
B) inches
C) inches
D) inches
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the reference angle for the given angle. -
A)
B)
C)
D)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Solve the right triangle shown in the figure. Round lengths to one decimal place and express angles to the nearest
tenth of a degree.  -A radio transmission tower is 230 feet tall. How long should a guy wire be if it is to be attached 9 feet from the top and is to make an angle of 35° with the ground? Give your answer to the nearest tenth of a foot.
-A radio transmission tower is 230 feet tall. How long should a guy wire be if it is to be attached 9 feet from the top and is to make an angle of 35° with the ground? Give your answer to the nearest tenth of a foot.
A) 385.3 feet
B) 401.0 feet
C) 269.8 feet
D) 280.8 feet
Correct Answer

verified
Correct Answer
verified
Showing 221 - 240 of 386
Related Exams