A) Polar coordinates:
B) Polar coordinates:
C) Polar coordinates:
D) Polar coordinates:
E) Polar coordinates:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. Vertices: (0,±2) ; asymptotes: y = ± x
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola.
A) Hyperbola
B) Circle
C) Parabola
D) Ellipse
E) None of the above
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center and vertices of the hyperbola and sketch its graph, using asymptotes as sketching aids.
A) Center: (0,0) Vertices: (-5,0) ![]()
B) Center: (0,0) Vertices: (-3,0) ![]()
C) Center: (0,0) Vertices: (3,0) ![]()
D) Center: (0,0) Vertices: (±5,0) ![]()
E) Center: (0,0) Vertices: (±3,0) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A) Symmetric with respect to , polar axis, poleCircle with radius ![]()
B) Symmetric with respect to , polar axis, poleCircle with radius ![]()
C) Symmetric with respect to , polar axis, poleCircle with radius ![]()
D) Symmetric with respect to , polar axis, poleCircle with radius ![]()
E) Symmetric with respect to , polar axis, poleCircle with radius ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex and directrix of the parabola.
A) vertex: directrix:
B) vertex: directrix:
C) vertex: directrix:
D) vertex: directrix:
E) vertex: directrix:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center and vertices of the hyperbola.
A) center: (-2, -4) , vertices: (-2, -6) , (-2, -2)
B) center: (2, 4) , vertices: (2, 2) , (2, 6)
C) center: (2, 4) , vertices: (0, 4) , (4, 4)
D) center: (-2, -4) , vertices: (-4, -4) , (0, -4)
E) center: (-4, -2) , vertices: (-6, -2) , (-2, -2)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select correct graph to graph rotated conic.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
The -coordinate system has been rotated degrees from the -coordinate system.The coordinates of a point in the -coordinate system are given.Find the coordinates of the point in the rotated coordinate system. ,
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Use the Quadratic Formula to solve for .
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the vertex and focus of the parabola.
A) vertex: focus:
B) vertex: focus:
C) vertex: (0, 0) focus:
D) vertex: (0, 0) focus:
E) vertex: (0, 0) focus:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Eliminate the parameter and write the corresponding rectangular equation whose graph represents the curve.
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Graph the hyperbola.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Sketch the graph of the ellipse, using the lateral recta.
A) ![]()
B) ![]()
C) ![]()
D) ![]()
E) ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
A) Symmetric with respect to the polar axis ![]()
B) Symmetric with respect to the polar axis ![]()
C) Symmetric with respect to the polar axis ![]()
D) Symmetric with respect to the polar axis ![]()
E) Symmetric with respect to the polar axis ![]()
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the angle (in radians and degrees) between the lines.Round your answer to four decimal places for radians and round your answer to one decimal places for degree.
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the center, vertices and foci of the hyperbola.
A) Center: (0, 0) Vertices: Foci:
B) Center: (0, 0) Vertices: Foci:
C) Center: (0, 0) Vertices: Foci:
D) Center: (0, 0) Vertices: Foci:
E) Center: (0, 0) Vertices: Foci:
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the standard form of the equation of the hyperbola with the given characteristics and center at the origin. Vertices: ; foci:
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
Find the angle (in radians and degrees) between the lines.Round your answer to four decimal places for radians and round your answer to one decimal places for degree. 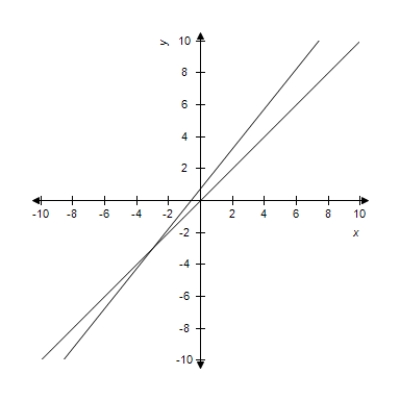
A)
B)
C)
D)
E)
Correct Answer

verified
Correct Answer
verified
Multiple Choice
By using a graphing utility select the correct graph of the polar equation.Identify the graph.
A) ![]() Hyperbola
Hyperbola
B) ![]() Hyperbola
Hyperbola
C) ![]() Hyperbola
Hyperbola
D) ![]() Hyperbola
Hyperbola
E) ![]() Hyperbola
Hyperbola
Correct Answer

verified
Correct Answer
verified
Showing 41 - 60 of 556
Related Exams